Capacitive Load
Apply a DC waveform to a circuit’s terminals, and its only impedance to current flow will be resistance. For an applied AC waveform, however, the situation becomes more complex. In addition to the resistive component – which remains constant irrespective of input waveform frequency – the circuit may exhibit inductive reactance, capacitive reactance or both. Inductive reactance is caused by items such as electric motors whose operation is based on alternating magnetic fields generated by coils. Capacitive reactance comes from devices with a dielectric that can store electrical charge.
Capacitive reactance is given by the equation
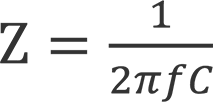
Where Z = reactance in Ohms, f = applied waveform frequency in Hertz and C = capacitance in Farads
This tells us that Z becomes infinite at 0 Hz (DC) so a capacitor appears as an open circuit to a DC current. It also shows that capacitive reactance decreases as frequency increases. These properties make capacitors useful for DC power supply smoothing as they provide a short circuit path for unwanted frequency signals. They are also found in AC filter circuits.
Additionally, capacitors draw current that leads the voltage sinusoidal waveform by 90° - they have a leading power factor. This contrasts with motors and other inductive machines that have a lagging power factor. Accordingly, capacitor banks can be added to systems with motors as a counteractive element to bring the power factor as close as possible to unity; this minimises the flow of unproductive, unwanted reactive currents in a circuit.